1 Getting Started with Karp, by Example
We start with a preliminary discussion of NP problems and reductions.
In Karp, reductions concern decision problems, that is, problems that have a "yes" or "no" answers. Two classic decision problems are \rm 3\text{-}S{\small AT} and \rm I{\small NDEPENDENT}\text{-}S{\small ET}. The first asks whether a 3-CNF formula is satisfiable. The second asks whether an undirected graph has at least k nodes that are not neighbors with each other.
We say that an instance of a decision problem is a yes-instance if there exists a certificate that verifies the “yes” answer. For instance, for an instance of \rm 3\text{-}S{\small AT}, that is a specifc 3-CNF formula, a certificate is a satisfying assignment that is a map from the variables of the formula to the booleans that makes the formula true. Similarly, for an instance of \rm I{\small NDEPENDENT}\text{-}S{\small ET}, that is an undirected graph and a natural number k, a certificate is a subset of the nodes of the graph that has at least size k and the nodes it contains are not neighbors.
If an instance has no certificate, then it is a no-instance.
We say a decision problem is in NP if there exist short certificates for all yes-instances, that is, there are ceritificates that can verify the “yes” answer in poly-time with respect to the size of the instance. Given a candidate certifcate for an instance, it is much easier to verify the “yes” or “no” answer than solving the actual instance. Hence, this definition admits both problems that we know how to solve easily, that is in poly-time, and hard problems for which we do not have poly-time algoritms.
A principled way to show that an NP decision problem, such as \rm I{\small NDEPENDENT}\text{-}S{\small ET}, is hard is with a correct reduction from a well-known NP-hard problem, such as \rm 3\text{-}S{\small AT}, to the problem whose “hardness” we investigate. A reduction is a function that given an instance of its from-problem constructs an instance of its to-problem. A correct reduction is a poly-time reduction that maps yes-instances to yes-instance and no-instances to no-instances. For instance, a correct reduction from \rm 3\text{-}S{\small AT} to \rm I{\small NDEPENDENT}\text{-}S{\small ET} maps (i) every 3-CNF formula with a satisfying assignment to an undirected graph that has an independent size of at least size k, for some k; and (ii) every 3-CNF that does not have a satisfying assignemnt to an an undirected graph that has no independent size of at least size k, for some k;
1.1 The Structure of Reductions in Karp
The two problem definitions of X and Y.
The forward instance construction, that is, the reduction itself which given an instance of X constructs an instance of Y.
In addition to these three pieces, for each reduction, Karp requires the definition of two additional functions that play the role of a proof argument about the correctness of the reduction:
The forward certificate construction consumes x, a yes-instance of X, and a certificate for x, and produces a certificate for y, the result of applying the forward instance construction from X to Y on x.
The backward certificate construction consumes x, a yes-instance of X, and a certificate for y, the result of applying the forward instance construction from X to Y on x, and produces a certificate for y.
In essence, if these two functions succeed in translating a certificate for any x to a certificate for the corresponding y and back, the forward instance construction is correct: it translates yes(no)-instances of X to yes(no)-instances of Y.
In the remainder of this section, we use the reduction from \rm 3\text{-}S{\small AT} to \rm I{\small NDEPENDENT}\text{-}S{\small ET} to demonstrate concretely the five pieces of a reduction in Karp.
1.2 Problem Definitions
Each problem definition is written as a separate module of the dedicated language karp/problem-definition.
#lang karp/problem-definition ; importing the karp cnf and mapping libraries (require karp/lib/cnf karp/lib/mapping) ; problem shape (decision-problem #:name 3sat #:instance ([φ is-a (cnf #:arity 3)]) #:certificate (mapping #:from (variables-of φ) #:to (the-set-of boolean))) ; verifier definition (define-3sat-verifier a-inst c^3sat (∀ [C ∈ (clauses-of (φ a-inst))] (∃ [l ∈ (literals-of C)] (or (and (positive-literal? l) (lookup c^3sat (underlying-var l))) (and (negative-literal? l) (not (lookup c^3sat (underlying-var l))))))))
Problem shape: The definition form decision-problem gives a name to the defined problem, and specifies the shape of its instances and certificates. For \rm 3\text{-}S{\small AT}, an instance is a 3-CNF formula φ, and a certificate a mapping from the variables of φ to the set of booleans.
Verifier definition: the definition of the problem shape generates a form for defining the certificate verifier of problem, that is a predicates that takes an instance and an alleged certificate, and checks if the alleged certificate is indeed a certificate of the given instance. In the running example, the define-3sat-verifier form checks if the given assignment c^3sat makes true at least one literal l of each clause C of the given instance a-inst.
(define foo (create-3sat-instance ([φ (cnf ('x1 ∨ 'x2 ∨ 'x3) ((¬'x1) ∨ (¬'x2) ∨ (¬'x3)) ((¬'x1) ∨ (¬'x2) ∨ 'x3))]))) (define foo-cert (mapping ('x1 ~> #f) ('x2 ~> #t) ('x3 ~> #f))) (3sat-verifier foo foo-cert) ;#t (define foo-non-cert (mapping ('x1 ~> #t) ('x2 ~> #t) ('x3 ~> #t))) (3sat-verifier foo foo-cert) ;#f (define foo-cert2 (3sat-solver foo)) (3sat-verifier foo foo-cert2) ;#t
#lang karp/problem-definition (require karp/lib/graph) ; problem structure definition (decision-problem #:name iset #:instance ([G is-a (graph #:undirected)] [k is-a natural]) #:certificate (subset-of (vertices-of G))) ; verifier definition (define-iset-verifier a-inst c^iset (and (>= (set-size c^iset) (k a-inst)) (∀ [u ∈ c^iset] (∀ [v ∈ (neighbors (G a-inst) u)] (set-∉ v c^iset)))))
(define V1 (set 'x1 'x2 'x3 'x4)) (define E1 (set ('x1 . -e- . 'x2) ('x1 . -e- . 'x3) ('x3 . -e- . 'x4) ('x2 . -e- . 'x3))) (define G1 (create-graph V1 E1))
(define/iset-instance iset-inst1 ([G G1] [k 2])) (iset-verifier iset-inst1 (set 'x1 'x4)) #; #t (iset-verifier iset-inst1 (set 'x1 'x3)) #; #f (define c^iset1 (iset-solver iset-inst1)) (iset-verifier iset-inst1 c^iset1) #; #t
1.3 Reduction
#lang karp/reduction ; importing the problem definitions and the libraries. (require (union-in "3sat.karp" "iset.karp") karp/lib/cnf karp/lib/graph karp/lib/mapping-reduction)
Recall that in a correct reduction from \rm 3\text{-}S{\small AT} to \rm I{\small NDEPENDENT}\text{-}S{\small ET} constructs an \rm I{\small NDEPENDENT}\text{-}S{\small ET} instance from a given \rm 3\text{-}S{\small AT} instance in the following steps:
Create a vertex for each literal in each clause of the CNF of the \rm 3\text{-}S{\small AT} instance:

Add the set of edges E1 that connects the vertices that correspond to literals that are negation of each other:
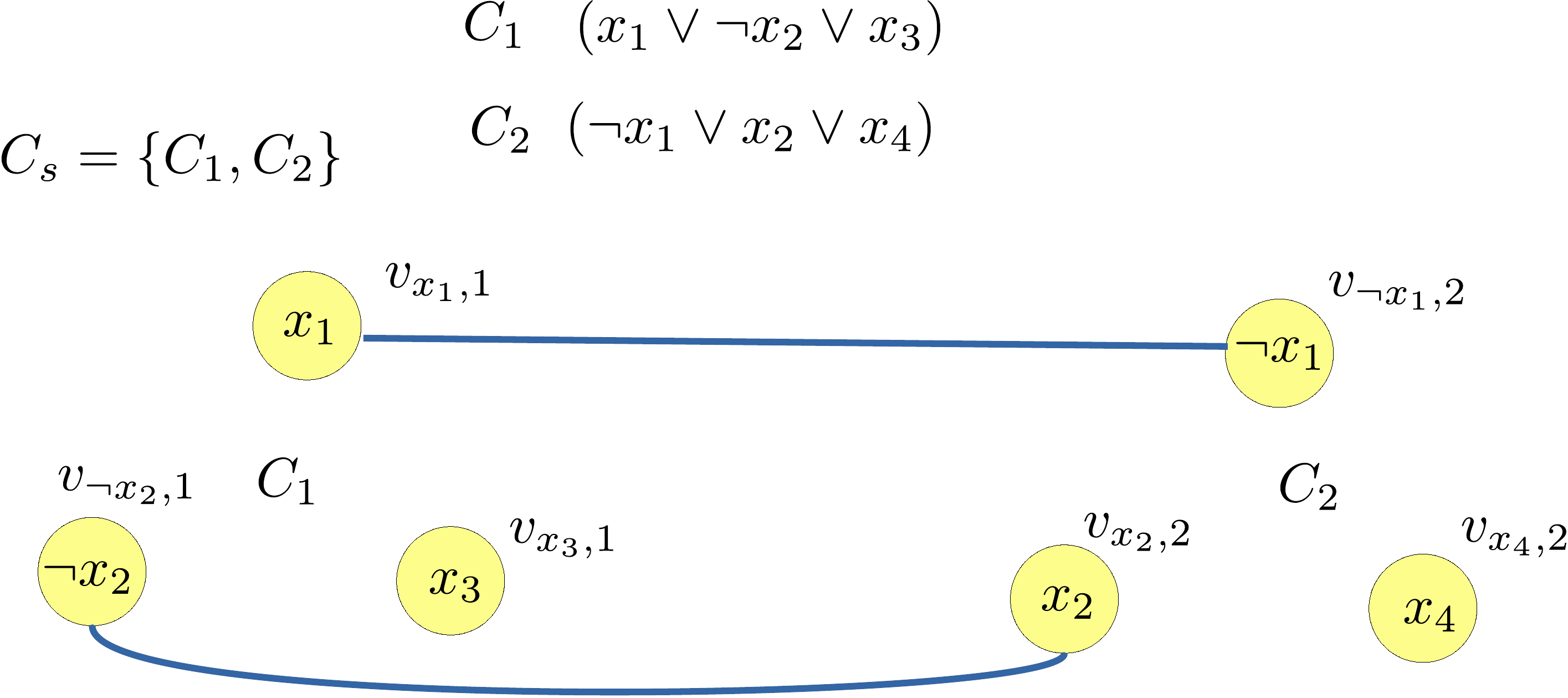
Add the set of edges E2 that connects the vertices that correspond to literals in the same clause.
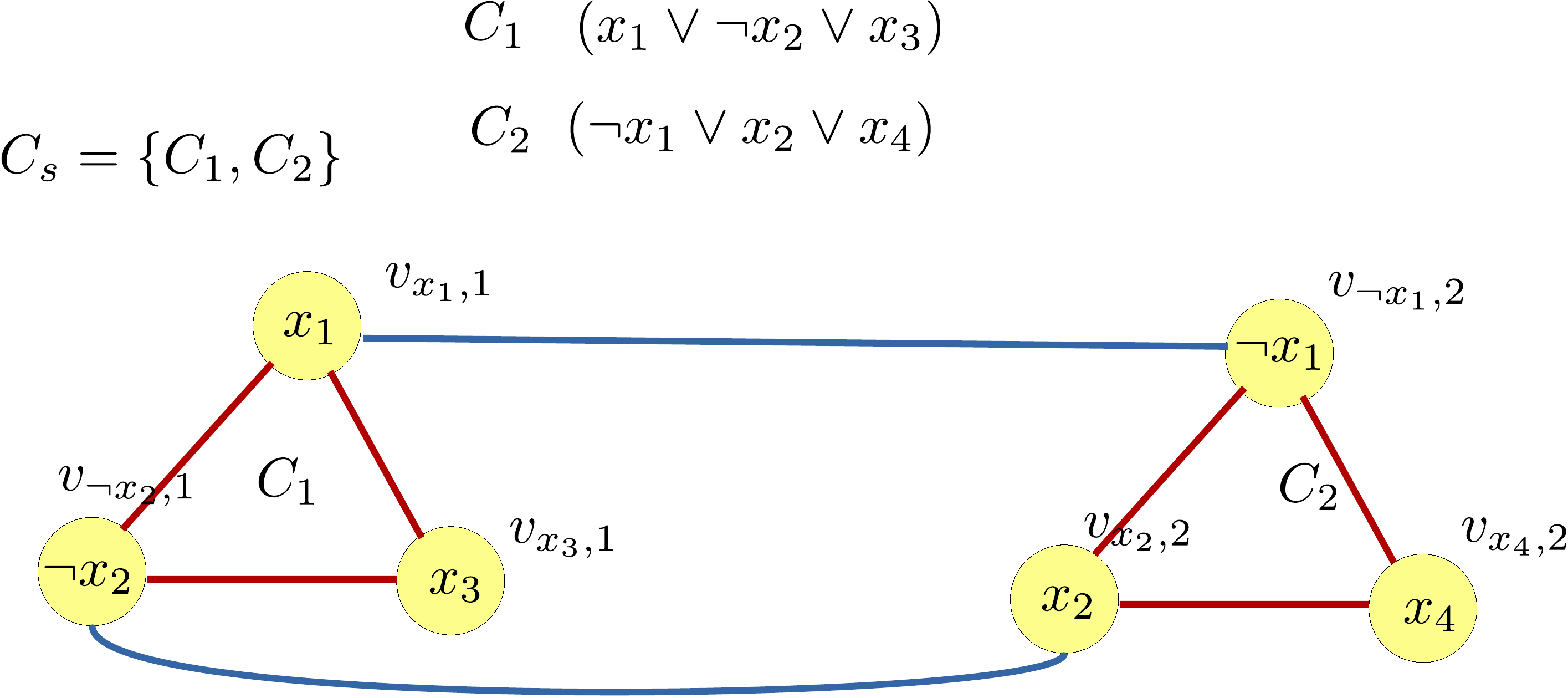
Finally, by putting the graph together and set the threshold k to be the number of clauses, we get the \rm I{\small NDEPENDENT}\text{-}S{\small ET} instance.
(define-forward-instance-construction #:from 3sat #:to iset (3sat->iset-v1 a-3sat-inst) (define Cs (clauses-of (φ a-3sat-inst))) ; creating the node for the graph (define V (for/set {(el l i) for [l ∈ C] for [(C #:index i) ∈ Cs]})) ; creating the set E1 for the graph (define E1 (for/set {((el l1 i) . -e- . (el l2 j)) for [l1 ∈ (literals-of C1)] for [l2 ∈ (literals-of C2)] for [(C1 #:index i) ∈ Cs] for [(C2 #:index j) ∈ Cs] if (literal-neg-of? l1 l2)})) ; creating the set E2 for the graph (define E2 (for/set {((el (fst p) i) . -e- . (el (snd p) i)) for [p ∈ (all-pairs-in (literals-of C))] for [(C #:index i) ∈ Cs]})) ; commenting out the E2 to introduce a mistake (create-iset-instance ([G (create-graph V (set-∪ E1 E2))] [k (set-size Cs)])))
In the definition of E1, we create each vertices as an abstract element el with first subscript being the literal itself and the second subscript being the index of the clause in the CNF that literal comes from.
[(C #:index i) ∈ Cs] binds the index of the current element C in question C in set Cs to i.
(-e- (el l1 i) (el l2 j)) creates an (undirected) edge with endpoints (el l1 i) and (el l2 j).
1.3.1 Forward Certificate Construction
The forward certificate construction maps a certificate of the from-problem instance to a certificate of the to-problem. It serves as a proof that a no-instance is always transformed to a no-instance.
To construct a certificate of \rm I{\small NDEPENDENT}\text{-}S{\small ET} from a certificate of \rm 3\text{-}S{\small AT},
we find one literal in each clause of the CNF that is satisfied
under the assignment and pick the vertices
corresponding to these literals to form the certificate.
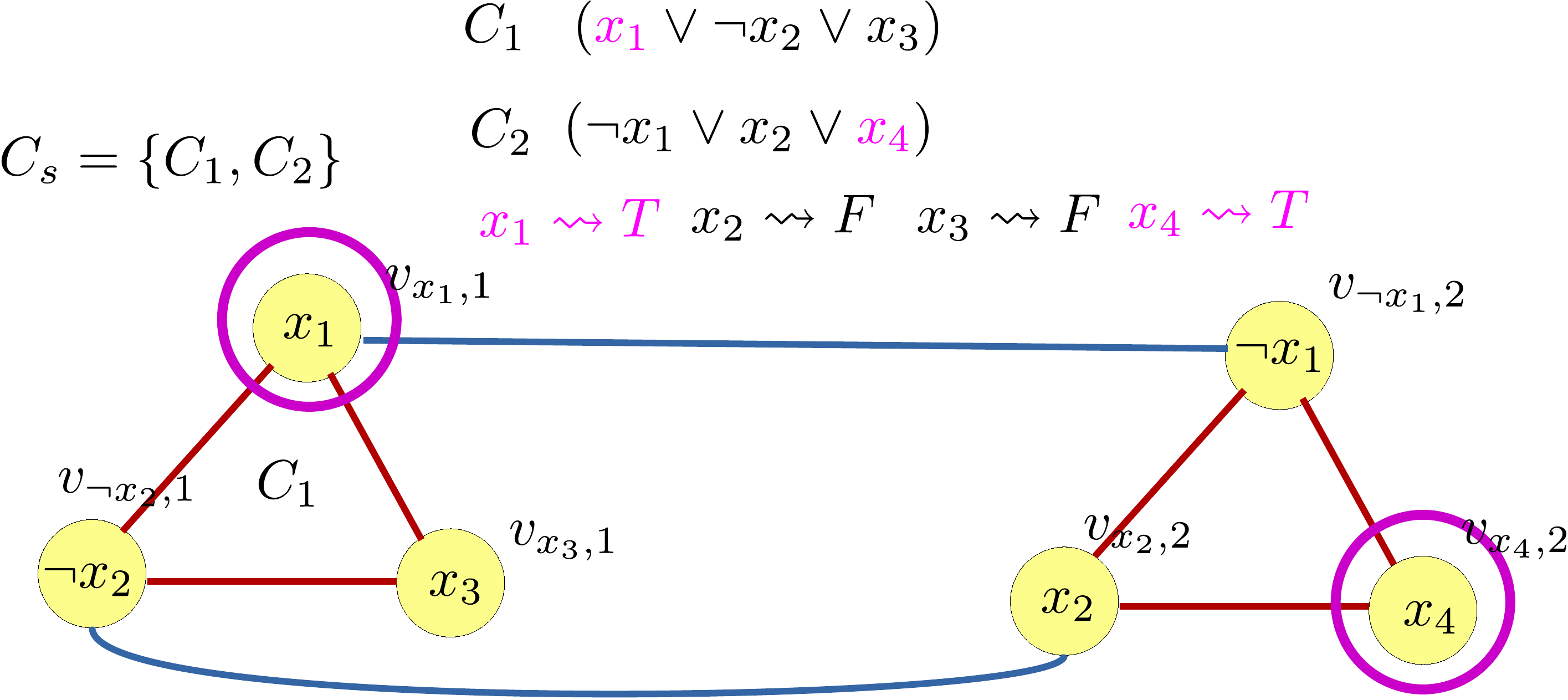
(define-forward-certificate-construction #:from 3sat #:to iset (3sat->iset->>-cert-v1 s->t-constr a-3sat-inst c^sat) ; getting the set of vertices from the assignment (for/set {(el (find-one [l ∈ C] s.t. (or (and (positive-literal? l) (lookup c^sat (underlying-var l))) (and (negative-literal? l) (not (lookup c^sat (underlying-var l)))))) i) for [(C #:index i) in (φ a-3sat-inst)]}))
an instance transformation function s->t-constr
a 3sat instance a-3sat-inst
a 3sat certificate c^sat, which is a mapping from the variables of a-3sat-inst to Booleans
1.3.2 Backward Certificate Construction
The backward certificate construction maps a certificate of the to-problem instance back to a certificate of the from-problem instance. It serves as a proof that a yes-instance is always transformed to a yes-instance.
To construct a \rm 3\text{-}S{\small AT} certificate from an \rm I{\small NDEPENDENT}\text{-}S{\small ET} certificate: We first find those variables that should be assigned to true. Each of these variable must be the underlying variable of some positive literal, the vertex correponding to which is in the independent set. We then create a mapping with these variables mapped to true and all other variables mapped to false. (The illustration is the same as the previous one)
(define-backward-certificate-construction #:from 3sat #:to iset (3sat->iset-<<-cert-v1 s->t-constr a-3sat-inst c^iset) (define X (variables-of (φ a-3sat-inst))) ; mapping back from vertices to assignments (define X-True (for/set {x for [x ∈ X] if (∃ [v in c^iset] (and (positive-literal? (_1s v)) (equal? (underlying-var (_1s v)) x)))})) (mapping [x ∈ X-True] ~> #t [x ∈ (set-minus X X-True)] ~> #f))
To extract the corresponding literal from the vertex, we use _1s to get the first subscript of the vertex, which is an abstract element as we defined in the instance construction.
1.3.3 Testing Reductions
(check-reduction #:from 3sat #:to iset 3sat->iset-v1 3sat->iset->>-cert-v1 3sat->iset-<<-cert-v1)
To see how a buggy reduction can be caught by the random testing, omitting the E2 in the instance construction and rerun check-reduction. (get-counterexample) can be used to access the \rm 3\text{-}S{\small AT} instance found as counterexample in the latest run of the check-reduction. To reproduce the testing results to help debugging, a random seed can be specified by adding an extra option #:random-seed to check-reduction.